반응형
[광고 누르면 오늘의 행운 상승!!]
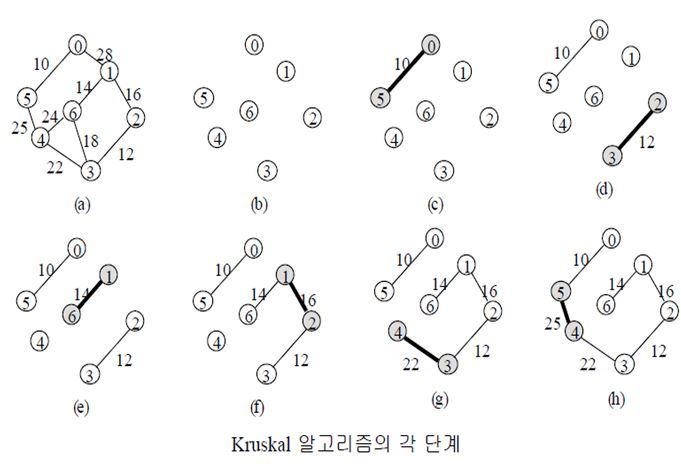
크루스칼 알고리즘 이란?
탐욕적인 방법(greedy method) 을 이용하여 그래프의 모든
정점을 최소 비용으로 연결하는 최소 비용을 구하는 것이다.
1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
3. 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.
<<UnionFind 를 이용하여 서로 다른 집합이면서 사이클이 형성되지 않는다면
간선을 추가하고 같은 집합으로 만든다.>>
package Study3;
import java.io.*;
import java.util.*;
public class bj_1700_최소스패닝트리_서울_06_박이삭_Kruskal{
static class Edge implements Comparable<Edge>{
int from;
int to;
int dis;
public Edge(int from, int to, int dis) {
this.dis = dis;
this.from = from;
this.to = to;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(this.dis, o.dis);
}
}
//x가 속한 집합의 부모를 찾는다.
public static int findSet(int[] p, int x) {
if (p[x] == x) return x;
else return p[x] = findSet(p, p[x]);
}
//x와 y를 같은 집합으로 합친다.
public static void union(int[] p, int x, int y) {
if (x < y) p[findSet(p, y)] = findSet(p, x);
else p[findSet(p, x)] = findSet(p, y);
}
static int V,E, ans = 0, cnt = 0;
static PriorityQueue<Edge> pq;
static int[] p;
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("test.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
//정점의 수
V = Integer.parseInt(st.nextToken());
//간선의 수
E = Integer.parseInt(st.nextToken());
pq = new PriorityQueue<>();
//정점을 저장할 배열
p = new int[V];
for (int i = 0; i < V; i++) {
p[i] = i;
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken())-1;
int b = Integer.parseInt(st.nextToken())-1;
int c = Integer.parseInt(st.nextToken());
pq.add(new Edge(a,b,c));
}
while(!pq.isEmpty()) {
Edge edge = pq.poll();
//from 노드와 to 노드의 부모가 같지 않다면
if (findSet(p, edge.from) != findSet(p, edge.to)) {
//거리를 증가시킨다.
ans+=edge.dis;
//모든 정점을 돌았으면 break;
if (++cnt == V) break;
//from과 to 노드를 합친다.
union(p, edge.from, edge.to);
}
}
System.out.println(ans);
}
}반응형
'6. 자료구조 이론 > 2. 비선형(Tree, Graph)' 카테고리의 다른 글
| 플로이드 와샬 알고리즘 [floydWarshall][JAVA] (0) | 2020.04.11 |
|---|---|
| Dijkstra 알고리즘 [다익스트라][최단거리][JAVA] (0) | 2020.04.11 |
| Prim 알고리즘 [프림][MST][JAVA] (1) | 2020.04.11 |
| 최소신장트리(MST) (0) | 2020.03.02 |
| 트리(Tree) (0) | 2020.03.02 |