반응형
[광고 누르면 오늘의 행운 상승!!]
트리란?
- 비선형 구조
- 원소들 간에 1:n 관계를 가지는 자료구조
- 원소들 간에 계층관게를 가지는 계층형 자료구조
- 상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무)모양의 구조
- 한 개 이상의 노드로 이루어진 유한 집합이며 다음 조건을 만족한다.
- 노드 중 최상위 노드를 루트(root)라고 한다.
- 나머지 노드들은 n(> = 0)의 분리 집합 T1,...,TN으로 분리될 수 있다.
- 이들 T1,...,TN은 각각 하나의 트리가 되며(재귀적 정의)루트의 부 트리(subtree)라고 한다.
노드
- 노드(node) - 트리의 원소 -트리 T의 노드 A,B,C,D,E,F,G,H,I,J,K
- 간선(edge) - 노드를 연결하는 선. 부모 노드와 자식 노드를 연결
- 루트 노드(root node) - 트리의 시작 노드
- 형제 노드(sibling node) - 같은 부모 노드의 자식 노드들
- B,C,D는 형제 노드
- 조상 노드 - 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들 - K의 조상 노드 : F,B,A
- 서브트리(subtree) - 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
- 자손 노드 - 서브 트리에 있는 하위 레벨의 노드들 -B의 자손 노드 -E,F,K

차수(degree)
- 노드의 차수 : 노드에 연결된 자식의 노드 수
- B의 차수 = 2 , C의 차수 = 1
- 트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값
- 트리 T의 차수 = 3
- 단말 노드(리프 노드) : 차수가 0인 노드, 자식 노드가 없는 노드
높이
- 노드의 높이 : 루트에서 노드에 이르는 간선의 수. 노드의 레벨
- B의 높이 = 1, F의 높이 = 2
- 트리의 높이 : 트리에 있는 노드의 높이 중에서 가장 큰 값. 최대 레벨
- 트리 T의 높이 = 3

이진트리
- 모든 노드들이 2개의 서브트리를 갖는 특별한 형태의 트리
- 각 노드가 자식 노드를 최대한 2개 까지만 가질 수 있는 트리 -왼쪽 자식 노드(left child node) -오른쪽 자식 노드(right child node)
- 레벨 n에서의 노드의 최대 개수는 2ⁿ개
- 높이가 n인 이진 트리가 가질 수 있는 노드의 최소 개수는 (n+1)개가 되며, 최대 개수는 (2ⁿ +¹ -1)개가 된다.

포화이진트리(perfect binary Tree)
- 모든 레벨에 노드가 포화상태로 차 있는 이진 트리
- 높이가 n일 때, 최대의 노드 개수인 (2ⁿ +¹ -1)의 노드를 가진 이진트리 - 높이 3일 때 (2³+¹ -1) 15개의 노드
- 루트를 1번으로 하여 (2ⁿ +¹ -1)까지 정해진 위치에 대한 노드 번호를 가짐
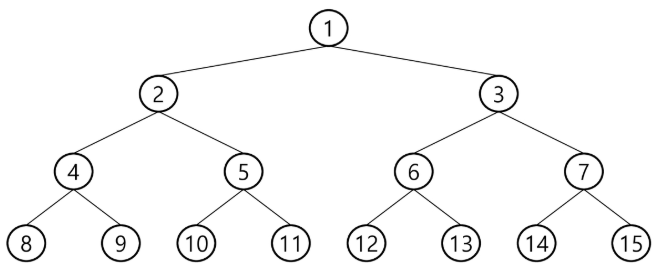
완전이진트리(Complete Binary Tree)
- 높이가 h이고 노드수가 n개일 때 포화 이진트리의 노드번호 1번부터 n번까지 빈 자리가 없는 이진 트리
- 예) 노드가 10개인 완전 이진 트리

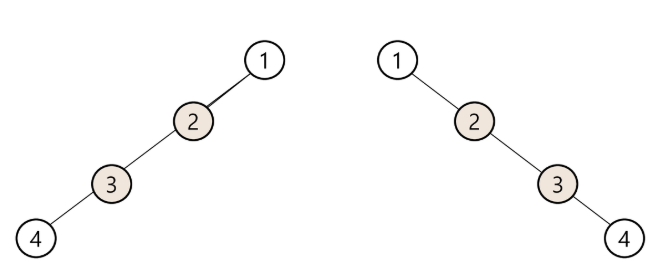
편향 이진 트리(Skewed Binary Tree)
- 높이 h에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드 만을 가진 이진 트리
- 왼쪽 편향 이진 트리
- 오른쪽 편향 이진 트리
이진트리 - 순회(traversal)
-
순회란?
순회(traversal) : 트리의 노드들을 체계적으로 방문하는 것
순회란 트리의 각 노드를 중복되지 않게 전부 방문(visit) 하는 것을 말하는데 트리는 비 선형 구조이기 때문에 선형구조에서와 같이 선후 연결 관계를 알 수 없다.
-
트리의 순회방법 3가지
전위순회(preorder traversal) : VLR
- 부모노드 방문 후, 자식노드를 좌,우 순서로 방문
중위순회(inorder traversal) : LVR
- 왼쪽 자식노드, 부모노드, 오른쪽 자식노드 순으로 방문한다.
후위순회(postorder traversal) : LRV
- 자식노드를 좌우 순서로 방문한 후, 부모노드로 방문한다.
전위순회(preorder traversal)
-
현재 노드 n을 방문하여 처리한다 →V
-
현재 노드 n의 왼쪽 서브트리로 이동한다. →L
-
현재 노드 n의 오른쪽 서브트리로 이동한다. →R
중위순회(inorder traversal)
-
현재 노드 n의 왼쪽 서브트리로 이동한다. →L
-
현재 노드 n을 방문하여 처리한다 →V
-
현재 노드 n의 오른쪽 서브트리로 이동한다. →R
후위순회(postorder traversal)
-
현재 노드 n의 왼쪽 서브트리로 이동한다. →L
-
현재 노드 n의 오른쪽 서브트리로 이동한다. →R
-
현재 노드 n을 방문하여 처리한다 →V
전위 순회 : A - B - D - H - I - E - J - C - F - K - G - L - M
중위 순회 : H - D - I - B - J - E - A - F - K - C - L - G - M
후위 순회 : H - I - D - J - E - B - K - F - L - M - G - C - A

구현소스
public class TreeTest {
static class Tree {
class Node {
char data;
Node left, right;
}
Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
public Node makeTree(Node left, char data, Node right) {
Node node = new Node();
node.left = left;
node.data = data;
node.right = right;
return node;
}
public void preorder(Node node) {
if (node != null) {
System.out.print(node.data + " ");
preorder(node.left);
preorder(node.right);
}
}
public void inorder(Node node) {
if (node != null) {
inorder(node.left);
System.out.print(node.data + " ");
inorder(node.right);
}
}
public void postorder(Node node) {
if (node != null) {
postorder(node.left);
postorder(node.right);
System.out.print(node.data + " ");
}
}
}
public static void main(String[] args) {
TreeTest.Tree t = new Tree();
// TreeTest.Tree.Node d = t.makeTree(null, 'D', null);
// TreeTest.Tree.Node h = t.makeTree(null, 'H', null);
// TreeTest.Tree.Node i = t.makeTree(null, 'I', null);
// TreeTest.Tree.Node f = t.makeTree(null, 'F', null);
// TreeTest.Tree.Node g = t.makeTree(null, 'G', null);
//
// TreeTest.Tree.Node e = t.makeTree(h, 'E', i);
// TreeTest.Tree.Node b = t.makeTree(d, 'B', e);
// TreeTest.Tree.Node c = t.makeTree(f, 'C', g);
// TreeTest.Tree.Node a = t.makeTree(b, 'A', c);
TreeTest.Tree.Node h = t.makeTree(null, 'H', null);
TreeTest.Tree.Node i = t.makeTree(null, 'I', null);
TreeTest.Tree.Node j = t.makeTree(null, 'J', null);
TreeTest.Tree.Node k = t.makeTree(null, 'K', null);
TreeTest.Tree.Node l = t.makeTree(null, 'L', null);
TreeTest.Tree.Node m = t.makeTree(null, 'M', null);
TreeTest.Tree.Node d = t.makeTree(h, 'D', i);
TreeTest.Tree.Node e = t.makeTree(j, 'E', null);
TreeTest.Tree.Node f = t.makeTree(null, 'F', k);
TreeTest.Tree.Node g = t.makeTree(l, 'G', m);
TreeTest.Tree.Node b = t.makeTree(d, 'B', e);
TreeTest.Tree.Node c = t.makeTree(f, 'C', g);
TreeTest.Tree.Node a = t.makeTree(b, 'A', c);
t.setRoot(a);
Tree.Node r = t.getRoot();
t.preorder(r);
System.out.println();
t.inorder(r);
System.out.println();
t.postorder(r);
System.out.println();
}
}반응형
'6. 자료구조 이론 > 2. 비선형(Tree, Graph)' 카테고리의 다른 글
| 플로이드 와샬 알고리즘 [floydWarshall][JAVA] (0) | 2020.04.11 |
|---|---|
| Dijkstra 알고리즘 [다익스트라][최단거리][JAVA] (0) | 2020.04.11 |
| Kruskal 알고리즘 [크루스칼][MST][JAVA] (0) | 2020.04.11 |
| Prim 알고리즘 [프림][MST][JAVA] (1) | 2020.04.11 |
| 최소신장트리(MST) (0) | 2020.03.02 |