반응형
다익스트라 알고리즘이란?
하나의 정점에서 다른 모든 정점들의 최단 경로를 구하는 알고리즘.
너비우선탐색(BFS)를 기본으로 한다.
간선들은 모두 양의 간선들을 가져야 한다.
첫 정점을 기준으로 연결되어 있는 정점들을 추가해가며, 최단 거리를 갱신하는 것.
정점을 잇기 전 까지는 시작점을 제외한 정점들은 모두 무한대를 가진다.
정점 A에서 정점B로 이어지면, 정점B가 가지는 최단거리는 시작점부터 정점A까지의 최단거리 +
점A와 점B간선의 가중치와, 기존에 가지고 있던 정점 B의 최단 거리중 작은 값이 B의 최단 거리가 된다.
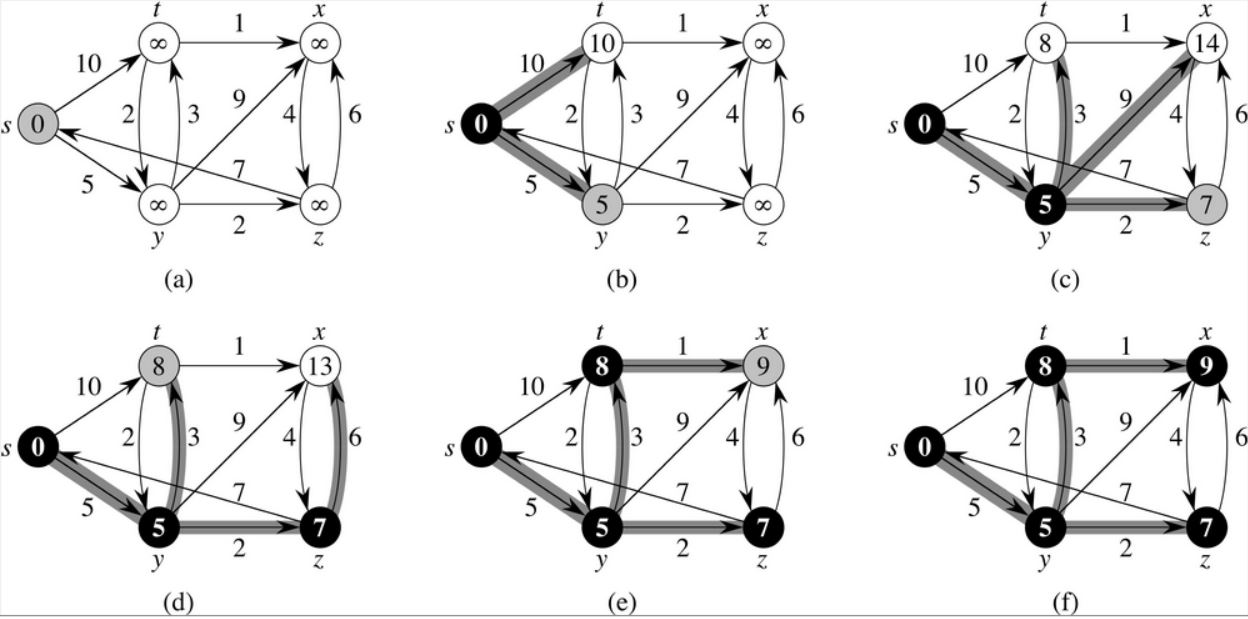
1. 배열을 이용한 다익스트라
package Study3;
import java.util.Arrays;
import java.util.Scanner;
public class 다익스트라 {
//pq X 간선이 매우 많을 때 유리
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int V = sc.nextInt(); //정점의 개수
int E = sc.nextInt(); //간선의 개수
int[][] adj = new int[V][V];
for (int i = 0; i < E; i++) {
adj[sc.nextInt()][sc.nextInt()] = sc.nextInt();
}
int[] D = new int[V];
Arrays.fill(D, Integer.MAX_VALUE);
boolean[] check = new boolean[V];
//dijkstra 시작점이 a정점이라면 D[a] = 0
D[0] = 0;
for (int i = 0; i < V-1; i++) {
int min = Integer.MAX_VALUE; // 가장 작은 값을 기억할 변수
int index = -1; //그 위치를 기억할 변수
for (int j = 0; j < V; j++) {
//아직 처리하지 않았으면서, 가장 짧은 거리면
if(!check[j] && min > D[j]) {
min = D[j];
index = j;
}
}
//새로운 친구로부터 갈수있는 경로들을 업데이트
for (int j = 0; j < V; j++) {
//!check[j], adj[index][j] != 0, D[index] + adj[index][j] < D[j]
if(!check[j] && adj[index][j] != 0 && D[index] + adj[index][j] < D[j])
D[j] = D[index] + adj[index][j];
}
//처리된놈으로 체크
check[index] = true;
}
System.out.println(Arrays.toString(D));
}
}
2. 우선순위 큐를 이용한 다익스트라
package Study3;
import java.util.*;
public class 다익스트라PQ {
static class Edge implements Comparable<Edge>{
int node, dis;
public Edge(int node, int dis) {
this.node = node;
this.dis = dis;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(this.dis, o.dis);
}
@Override
public String toString() {
return dis + "";
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int V = sc.nextInt();
int E = sc.nextInt();
List<Edge>[] graph = new ArrayList[V];
for (int i = 0; i < V; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < E; i++) {
//첫번째가 출발지, 두번째가 도착지, 세번째가 가중치
graph[sc.nextInt()].add(new Edge(sc.nextInt(), sc.nextInt()));
}
//dijkstra
PriorityQueue<Edge> pq = new PriorityQueue<>();
boolean[] visit = new boolean[V];
Edge[] D = new Edge[V];
//0번에서 출발하는 걸로
for (int i = 0; i < V; i++) {
//원하는 출발지
if( i == 0) {
//정점 0 번은 0으로 초기화
D[i] = new Edge(i,0);
}else {
//나머지 정점은 최대값으로 초기화
D[i] = new Edge(i, Integer.MAX_VALUE);
}
pq.add(D[i]);
}
while(!pq.isEmpty()) {
Edge edge = pq.poll();
if(edge.dis == Integer.MAX_VALUE) break;
for (Edge next : graph[edge.node]) {
// 방문했으면 x
if(visit[next.node]) continue;
// D[next.node]가 D[edge.node] + next.dis보다 더 크다면 갱신
if(D[next.node].dis > D[edge.node].dis + next.dis) {
D[next.node].dis = D[edge.node].dis + next.dis;
//pq에 갱신된 next를 넣기위해 기존 요소를 제거하고 다시 삽입
pq.remove(D[next.node]);
pq.add(D[next.node]);
}
}
//노드 방문체크
visit[edge.node] = true;
}
System.out.println(Arrays.toString(D));
}
}
반응형
'6. 자료구조 이론 > 2. 비선형(Tree, Graph)' 카테고리의 다른 글
| 플로이드 와샬 알고리즘 [floydWarshall][JAVA] (0) | 2020.04.11 |
|---|---|
| Kruskal 알고리즘 [크루스칼][MST][JAVA] (0) | 2020.04.11 |
| Prim 알고리즘 [프림][MST][JAVA] (1) | 2020.04.11 |
| 최소신장트리(MST) (0) | 2020.03.02 |
| 트리(Tree) (0) | 2020.03.02 |