반응형
최소신장트리(MST)
- 그래프에서 최소 비용 문제
- 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리
- 두 정점 사이의 최소 비용의 경로 찾기
- 신장 트리
- N개의 정점으로 이루어진 무향 그래프에서 N개의 정점과 N-1개의 간선으로 이루어진 트리
- 최소신장트리(Minimum Spanning Tree)
- 무향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리
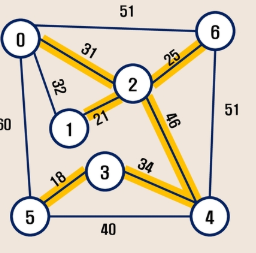
- 최소신장트리구하기
가중치가 적은 순서대로 나열한다.
(1,7)12 : (1의 부모는1, 7의부모는 7) 1를 부모로 설정 7의 부모는 1
(4,7)13 : (4의 부모는4, 7의 부모는 1) 4의 부모를 1로 설정
(1,5)17 : (1의 부모는 1, 5의 부모는 5) 5의 부모를 1로 설정
(3,5)20 : (3의 부모는 3, 5의 부모는 1) 3의 부모를 1로 설정
(2,4)24 : (2의 부모는 2, 4의 부모는 1) 2의 부모를 1로 설정
(1,4)28 : (1의 부모는 1, 4의 부모는 1) 선택하면 사이클이 되므로 선택 X
(3,6)37 : (3의 부모는 1, 6의 부모는 6) 6의 부모를 1로 설정
(5,6)45
(2,5)62
(1,2)67
(5,7)73
간선이 6개이므로 빠져나온다.
UnionFind(최소신장트리, 서로다른집합)
package graph;
import java.util.*;
public class UnionFind {
public static class Edge implements Comparable<Edge>{
int x,y,distance;
Edge(int x, int y, int distance){
this.x = x;
this.y = y;
this.distance = distance;
}
public String toString() {
return "(" + x + "," + y + ")" + distance;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(distance, o.distance); //거리가 작은 것 부터
}
}
public static void union(int[] p , int x, int y) {
x= findSet(p, x);
y= findSet(p, y);
if(x<y) p[y] = x;
else p[x] = y; // 그냥 우리가 정했어요~! 작은값을 parent로
}
public static boolean find(int[] p , int x, int y) {
return findSet(p, x) == findSet(p, y);
}
public static int findSet(int[] p, int x){
if(x == p[x]) return x;
return p[x] = findSet(p,p[x]); //이것을 넣고 안 넣고가 퍼포먼스의 큰 차이를 부른다.
}
public static void main(String[] args) {
int n = 7;
int m = 11;
List<Edge> g = new ArrayList<Edge>();
g.add(new Edge(1,7,12));
g.add(new Edge(1,4,28));
g.add(new Edge(1,2,67));
g.add(new Edge(1,5,17));
g.add(new Edge(2,4,24));
g.add(new Edge(2,5,62));
g.add(new Edge(3,5,20));
g.add(new Edge(3,6,37));
g.add(new Edge(4,7,13));
g.add(new Edge(5,6,45));
g.add(new Edge(5,7,73));
Collections.sort(g);
for(Edge e : g) System.out.println(e);
int[] p = new int[n+1]; //정점의 개수만큼 배열 생성
for(int i = 1; i <= n; i++) p[i] = i;
int sum = 0;
for (int i = 0; i < g.size(); i++) {
if(!find(p,g.get(i).x, g.get(i).y)) { //x의 부모와 y의 부모가 다르면 서로 다른 집합.
System.out.println("->" + g.get(i));
sum += g.get(i).distance;
union(p, g.get(i).x, g.get(i).y);
}
}
System.out.println(sum);
}
}Union int[] 방식
package graph;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collection;
import java.util.Collections;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
public class UnionFind1 {
//find-set
public static int findSet(int[] p, int x) {
if (x == p[x]) return x;
else return p[x] = findSet(p, p[x]);
}
//union
public static void union(int[] p, int x, int y) {
x = findSet(p, x);
y = findSet(p, y);
//작은 값을 대표자로 하도록 그냥 지정했음!
if (x < y) p[y] = x;
else p[x] = y;
}
//x와 y가 같은 집합인지 확인
public static boolean find(int[] p, int x, int y) {
return findSet(p, x) == findSet(p, y);
}
public static void main(String[] args) {
int n = 7;
int m = 11;
//1차원 배열 방식
List<int[]> g = new ArrayList<int[]>();
g.add(new int[]{1, 7, 12});
g.add(new int[] {1, 4, 28});
g.add(new int[] {1, 2, 67});
g.add(new int[] {1, 5, 17});
g.add(new int[] {2, 4, 24});
g.add(new int[] {2, 5, 62});
g.add(new int[] {3, 5, 20});
g.add(new int[] {3, 6, 37});
g.add(new int[] {4, 7, 13});
g.add(new int[] {5, 6, 45});
g.add(new int[] {5, 7, 73});
Collections.sort(g, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return Integer.compare(o1[2], o2[2]);
}
});
for (int[] arr : g) {
System.out.println(Arrays.toString(arr));
}
//make-set
int[] p = new int[n+1];
for (int i = 0; i <= n; i++) {
p[i] = i;
}
int sum = 0;
//g는 오름차순으로 정렬된 상태! 작은 것 부터 비교한다.
for (int i = 0; i < g.size(); i++) {
//다른 집합이라면!
if (!find(p, g.get(i)[0], g.get(i)[1])) {
System.out.println("->"+Arrays.toString(g.get(i)));
//가중치 통합
sum+=g.get(i)[2];
//x와 y를 합침
union(p, g.get(i)[0], g.get(i)[1]);
}
}
System.out.println(sum);
}
}반응형
'6. 자료구조 이론 > 2. 비선형(Tree, Graph)' 카테고리의 다른 글
| 플로이드 와샬 알고리즘 [floydWarshall][JAVA] (0) | 2020.04.11 |
|---|---|
| Dijkstra 알고리즘 [다익스트라][최단거리][JAVA] (0) | 2020.04.11 |
| Kruskal 알고리즘 [크루스칼][MST][JAVA] (0) | 2020.04.11 |
| Prim 알고리즘 [프림][MST][JAVA] (1) | 2020.04.11 |
| 트리(Tree) (0) | 2020.03.02 |